One of those cool effects used in oldskool demos is the Tunnel Effect. This
effect shows a tunnel in which you fly while the tunnel rotates, seemingly in
3D. This tutorial will explain how to make one.
How it works
An example tunnel looks like this, only in reality it animates:

The effect works as follows:
First, you need a texture, which is the texture of the sides of the tunnel.
The animation of the tunnel actually isn't calculated on the fly while the
animation runs, but it's precalculated. These calculations are stored in two
tables: one for the angle and one for the distance.
The distance table contains for every pixel of the screen, the inverse of the
distance to the center of the screen this pixel has. This gives pixels of the
center of the screen a very high value (those are very far away, as you can see
on the picture above), while the pixels on the sides of the screen get a low
value (these pixels represent parts of the tunnel close to the camera).
The angle table contains the angle of every pixel of the screen, where the
center of the screen represents the origin.
Then after everything is precalculated the animation loop starts. This animation
loop goes every frame, through every pixel (x,y), and then uses the angle and
distance table to ask which texel of the texture it should draw at the current
pixel. And, to get the animation, the values of the angle and distance table are
shifted: shifting the angle table makes the tunnel rotate, while shifting the
distance table makes you move forwards or backwards.
The texture has only a finite size, while the values gotten by the distance go
up to infinity, and the values of the angle are periodic. When a value outside
the texture is asked, modulo divide it through the size of the texture, this way
we get the texture repeated over and over (but always smaller as it's closer to
the center of the screen). You'll see this much better in the code.
The code
This code creates a tunnel where you fly forward while the tunnel rotates, and
the center of the tunnel always remains in the center of the screen. The code is
made so that no matter what size the texture has, the effect will always have
the same speed, and the texture is as big on the screen.
Here a few values are defined and buffers are created.
The texture array is the texture (duh). The bigger it's size, the better the
effect, I recommend making it at least 256*256 pixels, because it'll be as big
as the screen, and the rotation goes very shaky if the texture is too small.
The distanceTable is the precalculated table for the inverse distance of every
pixel, and the angleTable is the precalculated angle of every pixel. These have
to be at least as big as the screen, but if you also want to move the center of
the tunnel around on the screen, you'll have to make them bigger.
And the buffer array is used to draw the pixels to, so that the whole screen
buffer can be drawn at once instead of using pset for every separate pixel.
#define texWidth 256
#define texHeight 256
#define screenWidth 640
#define screenHeight 480
int texture[texWidth][texHeight];
int distanceTable[screenWidth][screenHeight];
int angleTable[screenWidth][screenHeight];
int buffer[screenWidth][screenHeight]; |
Here the main function starts, and a blue XOR texture is generated (you can also
load one from a bitmap instead).
int main(int argc, char *argv[])
{
screen(screenWidth, screenHeight, 0, "Tunnel Effect");
//generate texture
for(int x = 0; x < texWidth; x++)
for(int y = 0; y < texHeight; y++)
{
texture[x][y] = (x * 256 / texWidth) ^ (y * 256 / texHeight);
} |
Next the buffers are generated. The distance buffer uses the formula of the
inverse distance to the center of the screen (in 2D), multiplied by texHeight so
that no matter which size the texture has, it's always as big. It's also modulo
divided through texHeight so that the same texture is repeated all the time over
the whole distance.
The angle buffer calculates the angle of the current pixel (the angle it has to
the pixel in the center of the screen), by using the atan2 function. The atan2
function belongs to the <cmath> header, and returns the angle in radians of a
given point by giving it's x and y coordinate. It's divided through pi, so that
the texture will be wrapped exactly one time around the tunnel.
The ratio variable is the ratio between the width and height the texture will be
having on screen, or how long the texture stretches out in the distance.
//generate non-linear transformation table
for(int x = 0; x < w; x++)
for(int y = 0; y < h; y++)
{
int angle, distance;
float ratio = 32.0;
distance = int(ratio * texHeight / sqrt((x - w / 2.0) * (x - w / 2.0) + (y - h / 2.0) *
(y - h / 2.0))) % texHeight;
angle = (unsigned int)(0.5 * texWidth * atan2(y - h / 2.0, x - w / 2.0) / 3.1416);
distanceTable[x][y] = distance;
angleTable[x][y] = angle;
} |
Then the animation loop starts.
The animation variable is set to the time in seconds, and will be used for
shifting the tables for rotation and the moving.
Then for every pixel (x,y), the correct texel is gotten from the texture by
using the tables, and shifted with the animation value. The modulo division
through the width and height of the texture are to make sure we won't ask for a
pixel outside the texture, but use the same texture tiled instead. Unsigned
integers are used, because the values can become negative, and the modulo
division only works correctly if they're unsigned instead, so that negative
numbers will wrap around. Because of this, the texture width and height should
be powers of 2, or they won't nicely tile. The animation values (shiftX and
shiftY) are multiplied with the texture width and height to make the speed of
the effect independent of the texture size, only of the time.
The animation of the distance and angle is also multiplied with a constant value
(1.0 and 0.25 here), by changing these you can independently change the speed of
the rotation, and of the moving forward.
The pixels of the screen are drawn to the buffer, and after all pixels are
drawn, the buffer is put on screen, and the process restarts again for the next
frame.
float animation;
//begin the loop
while(!done())
{
animation = getTime() / 1000.0;
//calculate the shift values out of the animation value
int shiftX = int(texWidth * 1.0 * animation);
int shiftY = int(texHeight * 0.25 * animation);
for(int x = 0; x < w; x++)
for(int y = 0; y < h; y++)
{
//get the texel from the texture by using the tables, shifted with the animation values
int color = texture[(unsigned int)(distanceTable[x][y] + shiftX) % texWidth]
[(unsigned int)(angleTable[x][y] + shiftY) % texHeight];
buffer[x][y] = color;
}
drawBuffer(buffer[0]);
redraw();
}
return(0);
} |
This is what the tunnel looks like, but it also animates:
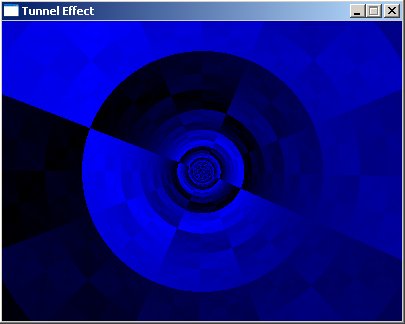
Better textures
Use this code instead of the code that generates the XOR pattern to load a
texture:
loadBMP("textures/tunnel.bmp", texture[0], texWidth, texHeight); |
Here are two textures from Unreal Tournament 2003 applied to the tunnel:

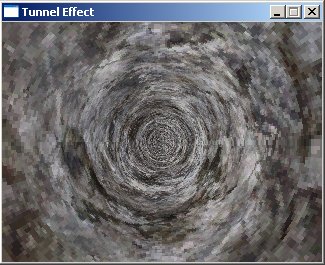

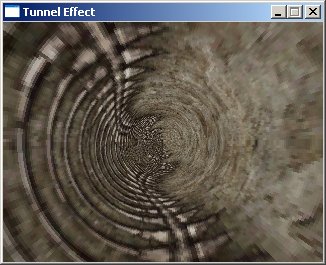
Looking Around
Because you keep moving forward all the time, the effect becomes boring fast. To
make it a bit more interesting, the camera can be made to look around. To do
this, simply move the center of the tunnel around, it then seems as if the
camera rotates. If you want to move the center of the tunnel around, bigger
precalculated buffers are needed. Here's a modified version of the code that'll
do this. The bold parts are new or changed, and the comments should explain it.
#define texWidth 256
#define texHeight 256
#define screenWidth 400
#define screenHeight 300
int texture[texWidth][texHeight];
//Make the tables twice as big as the screen. The center of the buffers is now the position (w,h).
int distanceTable[2 * screenWidth][2 * screenHeight];
int angleTable[2 * screenWidth][2 * screenHeight];
int buffer[screenWidth][screenHeight];
int main(int argc, char *argv[])
{
screen(screenWidth, screenHeight, 0, "Tunnel Effect");
loadBMP("textures/tunnel.bmp", texture[0], texWidth, texHeight);
//generate non-linear transformation table, now for the bigger buffers (twice as big)
for(int x = 0; x < w * 2; x++)
for(int y = 0; y < h * 2; y++)
{
int angle, distance;
float ratio = 32.0;
//these formulas are changed to work with the new center of the tables
distance = int(ratio * texHeight / sqrt(float((x - w) * (x - w) + (y - h) * (y - h)))) % texHeight;
angle = (unsigned int)(0.5 * texWidth * atan2(float(y - h), float(x - w)) / 3.1416);
distanceTable[x][y] = distance;
angleTable[x][y] = angle;
}
float animation;
//begin the loop
while(!done())
{
animation = getTime() / 1000.0;
//calculate the shift values out of the animation value
int shiftX = int(texWidth * 1.0 * animation);
int shiftY = int(texHeight * 0.25 * animation);
//calculate the look values out of the animation value
//by using sine functions, it'll alternate between looking left/right and up/down
//make sure that x + shiftLookX never goes outside the dimensions of the table, same for y
int shiftLookX = w / 2 + int(w / 2 * sin(animation));
int shiftLookY = h / 2 + int(h / 2 * sin(animation * 2.0));
for(int x = 0; x < w; x++)
for(int y = 0; y < h; y++)
{
//get the texel from the texture by using the tables, shifted with the animation variable
//now, x and y are shifted as well with the "look" animation values
int color = texture[(unsigned int)(distanceTable[x + shiftLookX][y + shiftLookY] + shiftX)
% texWidth][(unsigned int)(angleTable[x + shiftLookX][y + shiftLookY]+ shiftY) %
texHeight];
buffer[x][y] = color;
}
drawBuffer(buffer[0]);
redraw();
}
return(0);
} |
Here for example it's looking to the bottom left, so the center of the tunnel is
in the top right of the screen, but the looking direction changes all the time
while the effect runs:

If you're interested, because two sine functions are used to look around, one
for the looking in the x direction, and one for the looking in the y direction,
the look-around movement (or the path the center of the tunnel follows on the
screen) has the shape of a Lissajous figure.
