When drawing a 2D line on screen, it might happen that one or both of the
endpoints are outside the screen while a part of the line should still be
visible. In that case, an efficient algorithm is needed to find two new
endpoints that are on the edges on the screen, so that the part of the line
that's visible can now be drawn. This way, all those points of the line outside
the screen are clipped away and you don't need to waste any execution time on
them.
A good clipping algorithm is the Cohen-Sutherland algorithm. The function
containing this algorithm is already included in QuickCG in the file QuickCG.cpp
and is called clipLine. You pass the coordinates of the old line, and the
coordinates of the new line by reference so that the function can return the
coordinates of the new line by changing those parameters.
Clipping is a very important aspect of 3D graphics, and so in the 3D Lines
tutorial, this 2D Clipping function is used often.
Cohen Sutherland Clipping Algorithm
When drawing a 2D line, if one endpoint of the line is outside the screen, and
the other inside, you have to clip the line so that only the part of it that's
inside the screen remains. Even if both endpoints are outside the screen, it's
still possible that a part of the line should be visible. The clipping algorithm
needs to find new endpoints of the lines, that are inside or on the edges of the
screen. Here are a few cases, where the black rectangle represents the screen,
in red are the old endpoints, and in blue the ones after clipping:
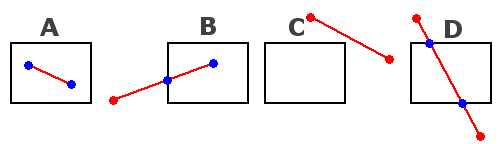
- Case A: both endpoints are inside the screen, no clipping needed.
- Case B: one endpoint outside the screen, that one had to be clipped
- Case C: both endpoint are outside the screen, and no part of the line is
visible, don't draw it at all.
- Case D: both endpoint are outside the screen, and a part of the line is
visible, clip both endpoints and draw it.
There are tons of different cases, each endpoint can be inside the screen, left
of it, right of it, above, below, etc... The Cohen Sutherland Clipping Algorithm
can recognize these cases quite efficiently and do the clipping. The algorithm
divides the 2D space in 9 regions:
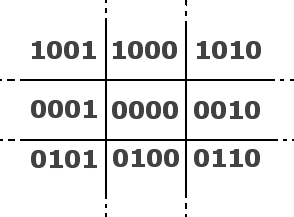
The center region is the screen, and the other 8 regions are on different sides
outside the screen. Each region is given a binary number, called an "outcode".
The codes are chosen as follows:
- If the region is above the screen, the first bit is 1
- If the region is below the screen, the second bit is 1
- If the region is to the right of the screen, the third bit is 1
- If the region is to the left of the screen, the fourth bit is 1
Obviously an area can't be to the left and the right at the same time, or above
and below it at the same time, so the third and fourth bit can't be 1 together,
and the first and second bit can't be 1 together. The screen itself has all 4
bits set to 0.
Both endpoints of the line can lie in any of these 9 regions, and there are a
few trivial cases:
- If both endpoints are inside or on the edges of the screen, the line is
inside the screen or clipped, and can be drawn. This case is the trivial
accept.
- If both endpoints are on the same side of the screen (e.g., both
endpoints are above the screen), certainly no part of the line can be
visible on the screen. This case is thetrivial reject, and the line
doesn't have to be drawn.
These two cases can easily be detected thanks to the outcodes of the regions:
- Trivial Accept: both endpoints have to be in the region with code 0000,
so the trivial accept case only happens if code1 | code2 == 0,
where code1 and code2 are the codes of both endpoints of the line, and '|'
is the binary OR operator, which can only return 0 if both codes are 0.
- Trivial Reject: because of the way the codes of the regions were chosen,
only if both endpoints of the line are on the same side of the region, both
codes will have two corresponding bits that are both 1. For example, only if
both endpoints are on the left of the screen, the fourth bit of both codes
is 1. So, the trivial reject case is detected if code1 & code2 != 0,
where & is the binary AND operation. The binary AND operation only returns a
non zero result if two corresponding bits are 1.
All other cases (i.e. no trivial reject and no trivial accept) have to be turned
into a trivial case by doing one clip operation. The Cohen Sutherland algorithm
is a loop, that does only one clipping operation at the time. It can clip one
endpoint of the line, and only clip it to a vertical or horizontal region
border. In many cases, it has to clip multiple times before it can finally
detect if the line is to be accepted, or rejected. It never has to be clipped
more than about 4 times though, so it's quite fast.
The function that uses the Cohen Sutherland Clipping Algorithm is the clipLine
function from QuickCG, which is in the QuickCG.cpp file. It uses an auxiliary
function, findRegion, that returns the binary code of the region a given
endpoint is in. For example to set the second bit to 1, you have to 'OR' the
code with 4 (the first bit represents 8, the second 4, the third 2, and the
firth (the primary bit) represents 1).
int findRegion(int x, int y)
{
int code=0;
if(y >= h)
code |= 1; //top
else if( y < 0)
code |= 2; //bottom
if(x >= w)
code |= 4; //right
else if ( x < 0)
code |= 8; //left
return(code);
}
|
The clipLine function loop starts with detecting if there's a trivial case:
bool clipLine(int x1, int y1, int x2, int y2, int & x3, int & y3, int & x4, int & y4)
{
int code1, code2, codeout;
bool accept = 0, done=0;
code1 = findRegion(x1, y1); //the region outcodes for the endpoints
code2 = findRegion(x2, y2);
do //In theory, this can never end up in an infinite loop, it'll always come in one of the
trivial cases eventually
{
if(!(code1 | code2)) accept = done = 1; //accept because both endpoints are in screen
or on the border, trivial accept
else if(code1 & code2) done = 1; //the line isn't visible on screen, trivial reject
|
If no trivial case was detected, the line has to be clipped. Only one of the 4
possible clipping operations is done at the time. To clip, one coordinate of 1
endpoint is set to one of the borders of the regions, which also happen to be
the coordinates of borders of the screen, and the other coordinate of that point
is recalculated by filling in the equation of the line. To detect which clipping
operation has to be performed, an endpoint that's
not inside the screen has to be chosen.
The code of that endpoint is called codeout, and is set to either code1 or code2
depending on which of those isn't zero.
else //if no trivial reject or accept, continue the loop
{
int x, y;
codeout = code1 ? code1 : code2;
if(codeout & 1) //top
{
x = x1 + (x2 - x1) * (h - y1) / (y2 - y1);
y = h - 1;
}
else if(codeout & 2) //bottom
{
x = x1 + (x2 - x1) * -y1 / (y2 - y1);
y = 0;
}
else if(codeout & 4) //right
{
y = y1 + (y2 - y1) * (w - x1) / (x2 - x1);
x = w - 1;
}
else //left
{
y = y1 + (y2 - y1) * -x1 / (x2 - x1);
x = 0;
}
|
The part above calculated the new coordinates of the clipped point, and now the
coordinates have to be set to endpoint1 or endpoint2 depending which endpoint
codeout represented. This is also the end of the loop, after this either the
line entered a trivial case, or it's still not a trivial case and the loop is
performed again to do more clipping.
if(codeout == code1) //first endpoint was clipped
{
x1 = x; y1 = y;
code1 = findRegion(x1, y1);
}
else //second endpoint was clipped
{
x2 = x; y2 = y;
code2 = findRegion(x2, y2);
}
}
}
while(done == 0);
|
After the loop and thus the clipping is done, the function sets the 4
coordinates of the new line (which were passed to the function by reference) and
returns whether or not we had a trivial accept or a trivial reject.
if(accept)
{
x3 = x1;
x4 = x2;
y3 = y1;
y4 = y2;
return 1;
}
else
{
x3 = x4 = y3 = y4 = 0;
return 0;
}
}
|
