To generate a sky with clouds, you can use the turbulence texture above, but
with a blue-white color palette instead of black and white. For that the
HSLtoRGB function can be used, with the hue set to blue (169 or 240�) and
lightness ranging from 192 to 255 to make it white enough. Here's a new main
function that'll do this:
#define noiseWidth 320
#define noiseHeight 240
double noise[noiseWidth][noiseHeight]; //the noise array
void generateNoise();
double smoothNoise(double x, double y);
double turbulence(double x, double y, double size);
int main(int argc, char *argv[])
{
screen(noiseWidth, noiseHeight, 0, "Random Noise");
generateNoise();
Uint8 L;
ColorRGB color;
for(int x = 0; x < w; x++)
for(int y = 0; y < h; y++)
{
L = 192 + Uint8(turbulence(x, y, 64)) / 3;
color = HSLtoRGB(ColorHSL(169, 255, L));
pset(x, y, color);
}
redraw();
sleep();
return 0;
} |
The division of the turbulence result through 3 (instead of 4) might give a
value that's too large for a pixel color parameter, but usually it doesn't and
it gives brighter clouds:

Marble
It's possible to use random Noise to create a texture that looks like marble. To
do this, a sine pattern is taken as base, a sine pattern looks like this:

The sine texture is generated by giving the pixel at position (x, y) the color
value 255 * sin(x + y). You can change the angle and period (= amount of lines)
by multiplying x and y with factors. The sine pattern has dark and bright
lines, and by applying turbulence to these lines by adding a turbulence term in
the sine, you get something that looks like the veins of marble:
int main(int argc, char *argv[])
{
screen(noiseWidth, noiseHeight, 0, "Marble");
generateNoise();
ColorRGB color;
//xPeriod and yPeriod together define the angle of the lines
//xPeriod and yPeriod both 0 ==> it becomes a normal clouds or turbulence pattern
double xPeriod = 5.0; //defines repetition of marble lines in x direction
double yPeriod = 10.0; //defines repetition of marble lines in y direction
//turbPower = 0 ==> it becomes a normal sine pattern
double turbPower = 5.0; //makes twists
double turbSize = 32.0; //initial size of the turbulence
for(int x = 0; x < w; x++)
for(int y = 0; y < h; y++)
{
double xyValue = x * xPeriod / noiseHeight + y * yPeriod / noiseWidth + turbPower *
turbulence(x, y, turbSize) / 256.0;
double sineValue = 256 * fabs(sin(xyValue * 3.14159));
color.r = color.g = color.b = Uint8(sineValue);
pset(x, y, color);
}
redraw();
sleep();
return 0;
} |
The value "xyValue" is the sum of x multiplied with a factor, y multiplied with
a factor, and the turbulence multiplied with a factor. xPeriod, yPeriod and
turbPower are parameters that you can change to get different textures. The
division through 256 of the turbulence is done to bring it to a value between 0
and 1, because the turbulence function was made to return values from 0 to 255.
The values above give the following result:

Decreasing turbPower will give less twists, for example if you set it to 1.0,
you get:

You can see much better how a sine pattern is used now, the dark and bright
lines only twist a small bit, which still gives a sort of natural look.
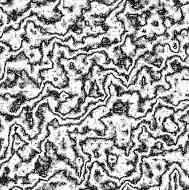
Changing the initial size of the turbulence function makes the twists bigger
(and thus much more subtle, similar to making turbPower smaller), while a small
initial size gives much smaller but mor eaggressive twists. Here turbPower is
set to 5.0 again, and turbSize to128.0 and 16.0 respectively:

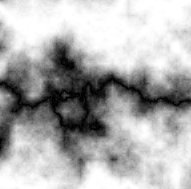
Changing the period of x and y makes more or less black lines, for example here
the lines are made wider and with an angle of 0� by setting xPeriod to 0 and
yPeriod to 1 so that there'll be only one horizontal black line. turbSize is set
to 32, and turbPower to only 1 so that you can see the direction of the line
better:
Here are the same parameters, but turbPower back to 5, so you can see how a big
enough turbulence really totally hides the fact that there's only one black
line:
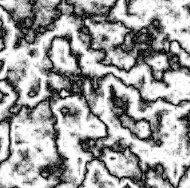
You can also change the colors of the marble by using a different value for R, G
and B, for example to make it a bit red or yellowish:
double xyValue = x * xPeriod / noiseHeight + y * yPeriod / noiseWidth + turbPower *
turbulence(x, y, turbSize) / 256.0;
double sineValue = 226 * fabs(sin(xyValue * 3.14159));
color.r = Uint8(30 + sineValue);
color.g = Uint8(10 + sineValue);
color.b = Uint8(sineValue);
pset(x, y, color); |

By playing around with the parameters you can get totally different marble or
stone patterns.
Wood
Natural looking rings of wood can be created by adding turbulence to the
following mathematical function:

To get the pattern above, take the sine of the distance of x and y to the
center, so the color of the pixel at position x, y is 256 * sin(sqrt(x*x +
y*y)). Add a turbulence term into the sine, and you get natural looking wood.
The values R, G and B are calculated out of the result in such a way that the
wood will look brown:
int main(int argc, char *argv[])
{
screen(noiseWidth, noiseHeight, 0, "Wood");
generateNoise();
ColorRGB color;
double xyPeriod = 12.0; //number of rings
double turbPower = 0.1; //makes twists
double turbSize = 32.0; //initial size of the turbulence
for(int x = 0; x < w; x++)
for(int y = 0; y < h; y++)
{
double xValue = (x - noiseHeight / 2) / double(noiseHeight);
double yValue = (y - noiseWidth / 2) / double(noiseWidth);
double distValue = sqrt(xValue * xValue + yValue * yValue) + turbPower *
turbulence(x, y, turbSize) / 256.0;
double sineValue = 128.0 * fabs(sin(2 * xyPeriod * distValue * 3.14159));
color.r = Uint8(80 + sineValue);
color.g = Uint8(30 + sineValue);
color.b = 30;
pset(x, y, color);
}
redraw();
sleep();
return 0;
} |
The rings are supposed to be visible here so, unlike for the marble, turbPower
should be small.

Here's the result with more rings: xyPeriod is set to 25.

Here the wood has 12 rings again, but more turbulence: turbPower is set to 0.2:

If you make turbPower too high, the rings won't be visible anymore, and you'll
get something that looks more like the marble patterns. Here it's set to 0.5:

So you see how you can turn a mathematical 2D function into a natural looking
texture by adding noise to it. You can try this on much more functions, for
example here's the mathematical pattern sin(x) + sin(y):

Add some noise to it with the following code:
double xValue = (x - noiseHeight / 2) / double(noiseHeight) + turbPower *
turbulence(x, y, turbSize) / 256.0;
double yValue = (y - noiseWidth / 2) / double(noiseWidth) + turbPower *
turbulence(h - y, w - x, turbSize) / 256.0;
double sineValue = 22.0 * fabs(sin(xyPeriod * xValue * 3.1415) + sin(xyPeriod *
yValue * 3.1415));
color = HSVtoRGB(ColorHSV(Uint8(sineValue), 255, 255));
pset(x, y, color); |
And you get:

2D random noise can also be used for terrain heightmaps, physical simulations,
etc...
3D Random Noise
Random Noise can be extended to any number of dimensions. The extension to 3D
requires adding a z component, apart from a width and height the noise array now
also needs a depth.
#define noiseWidth 192
#define noiseHeight 192
#define noiseDepth 64
double noise[noiseWidth][noiseHeight][noiseDepth]; //the noise array |
The generateNoise function now needs to fill up the 3-dimensional array so it
gets an extra loop:
void generateNoise()
{
for(int x = 0; x < noiseWidth; x++)
for(int y = 0; y < noiseHeight; y++)
for(int z = 0; z < noiseDepth; z++)
{
noise[x][y][z] = (rand() % 32768) / 32768.0;
}
} |
The smoothing function now has to interpolate in the x, y and z direction so
there are 8 terms instead of only 4:
double smoothNoise(double x, double y, double z)
{
//get fractional part of x and y
double fractX = x - int(x);
double fractY = y - int(y);
double fractZ = z - int(z);
//wrap around
int x1 = (int(x) + noiseWidth) % noiseWidth;
int y1 = (int(y) + noiseHeight) % noiseHeight;
int z1 = (int(z) + noiseDepth) % noiseDepth;
//neighbor values
int x2 = (x1 + noiseWidth - 1) % noiseWidth;
int y2 = (y1 + noiseHeight - 1) % noiseHeight;
int z2 = (z1 + noiseDepth - 1) % noiseDepth;
//smooth the noise with bilinear interpolation
double value = 0.0;
value += fractX * fractY * fractZ * noise[x1][y1][z1];
value += fractX * (1 - fractY) * fractZ * noise[x1][y2][z1];
value += (1 - fractX) * fractY * fractZ * noise[x2][y1][z1];
value += (1 - fractX) * (1 - fractY) * fractZ * noise[x2][y2][z1];
value += fractX * fractY * (1 - fractZ) * noise[x1][y1][z2];
value += fractX * (1 - fractY) * (1 - fractZ) * noise[x1][y2][z2];
value += (1 - fractX) * fractY * (1 - fractZ) * noise[x2][y1][z2];
value += (1 - fractX) * (1 - fractY) * (1 - fractZ) * noise[x2][y2][z2];
return value;
} |
The turbulence function is easy to extend, just add z / size to the call to the
smoothNoise function:
double turbulence(double x, double y, double z, double size)
{
double value = 0.0, initialSize = size;
while(size >= 1)
{
value += smoothNoise(x / size, y / size, z / size) * size;
size /= 2.0;
}
return(128.0 * value / initialSize);
} |
The main function presented here will use the 3D random noise to generate clouds
animated in the time. It's as if the clouds are forming and changing smoothly.
int main(int argc, char *argv[])
{
screen(noiseWidth, noiseHeight, 0, "3D Random Noise");
generateNoise();
Uint8 L;
ColorRGB color;
double t;
while(!done())
{
for(int x = 0; x < w; x++)
for(int y = 0; y < h; y++)
{
L = 192 + Uint8(turbulence(x, y, t, 32)) / 4;
color = HSLtoRGB(ColorHSL(169, 255, L));
pset(x, y, color);
}
t = getTime() / 40.0;
redraw();
}
return 0;
} |
The screenshot can't show how it animates of course:

3D andom noise can be used for animating 2D textures, for 3D textures (3D
textures can for example be used on a rock of which you can remove parts or
shoot pieces off it to see the inside of it, if you'd lay a 2D on it, and you
remove a part of it, that same 2D texture would be drawn again), 3D planet
textures, 3D volumetric fog, etc...
