In nature, everything has a random look, while mathematical formulas typically don't generate random looking results, unless you use them well. Random noise, such as Perlin noise invented by Ken Perlin, uses random numbers to generate natural looking textures.

Smooth Noise

As source for the random noise we need an array of random values, called noise[x][y]. Since our interest is generating 2D textures, a 2D array is used. The function generateNoise will fill the array with noise, and the main function is programmed to show this noise array on the screen. The noise itself is generated with the rand() function from the <cstdlib> header file, this function returns a random integer value between 0 and 32768 (as defined in the header file). It's normalized to a random real number between 0 and 1 by dividing it through 32768.0 (make sure to use floating point division).

#define noiseWidth 128
#define noiseHeight 128

double noise[noiseWidth][noiseHeight]; //the noise array

void generateNoise();

int main(int argc, char *argv[])
{
    screen(noiseWidth, noiseHeight, 0, "Random Noise");
    generateNoise();
    
    ColorRGB color;
     
    for(int x = 0; x < w; x++)
    for(int y = 0; y < h; y++)
    {     
        color.r = color.g = color.b = Uint8(256 * noise[x][y]);
        pset(x, y, color);
    }  
    
    redraw();
    sleep();
    return 0;
}

void generateNoise()
{
    for (int x = 0; x < noiseWidth; x++)
    for (int y = 0; y < noiseHeight; y++)
    {
        noise[x][y] = (rand() % 32768) / 32768.0;
    }
}

		color.r = color.g = color.b = Uint8(256 * noise[x / 8][y / 8]);
        pset(x, y, color);

double smoothNoise(double x, double y)
{  
   //get fractional part of x and y
   double fractX = x - int(x);
   double fractY = y - int(y);
   
   //wrap around
   int x1 = (int(x) + noiseWidth) % noiseWidth;
   int y1 = (int(y) + noiseHeight) % noiseHeight;
   
   //neighbor values
   int x2 = (x1 + noiseWidth - 1) % noiseWidth;
   int y2 = (y1 + noiseHeight - 1) % noiseHeight;

   //smooth the noise with bilinear interpolation
   double value = 0.0;
   value += fractX       * fractY       * noise[x1][y1];
   value += fractX       * (1 - fractY) * noise[x1][y2];
   value += (1 - fractX) * fractY       * noise[x2][y1];
   value += (1 - fractX) * (1 - fractY) * noise[x2][y2];

   return value;
}

 
		color.r = color.g = color.b = Uint8(256 * smoothNoise(x / 8.0, y / 8.0));
        pset(x, y, color);

Turbulence

Turbulence is what creates natural looking features out of smoothed noise. The trick is to add multiple noise textures of different zooming scales together. An example of how this represents nature can be found in a mountain range: there are very large features (the main mountains), they are very deeply zoomed in noise.



Then added to the mountains are smaller features: multiple tops, variations in the slope, ...



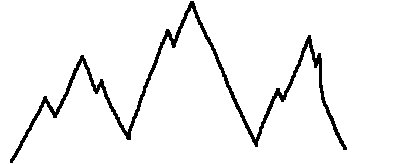
Then, at an even smaller scale, there are rocks on the mountains.



An even smaller layer is the grains of sand. Together, the sum of all these layers forms natural looking mountains.

In 2D, this is done by adding different sizes of the smoothed noise together.



The zooming factor started at 16 here, and is divided through two each time. Keep doing this until the zooming factor is 1. The small features in the mountain example weren't only smaller in the width, but also in the height. To achieve this in 2D textures, make the images with a smaller zoom darker, so adding them will have less effect:



By adding these 5 images together, and dividing the result through 5 to get the average, you get a turbulence texture:



Here's a function that'll automaticly do all this for a single pixel. The parameter "size" is the initial zoom factor, which was 16 in the example above. The return value is normalized so that it'll be a number between 0 and 255.

double turbulence(double x, double y, double size)
{
    double value = 0.0, initialSize = size;
    
    while(size >= 1)
    {
        value += smoothNoise(x / size, y / size) * size;
        size /= 2.0;
    }
    
    return(128.0 * value / initialSize);
}

        color.r = color.g = color.b = Uint8(turbulence(x, y, 64));
        pset(x, y, color);