|
L'ultima struttura di dati che studeremo in questa lezione privata � i Graphs. I Graphs sono simili agli Trees salvo che, non hanno altretante limitazioni. Nella lezione privata precedente, abbiamo visto che ogni albero ha un nodo della radice e tutti i altri nodi nell'albero sono bambini di un nodo perticular. Inoltre abbiamo visto che i nodi possono avere molti bambini ma soltanto un genitore. Quando ci distendiamo queste limitazioni, otteniamo la struttura di dati del Graph. La rappresentazione logica di un Graph tipico ha potuto osservare qualcosa come la figura indicata qui sotto:
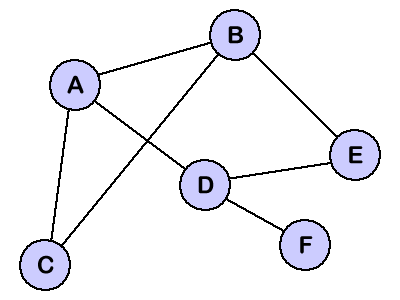
Notare che il nostro Graph non ha alcun nodo della radice come la struttura di dati dell'albero. Invece, tutto il nodo pu� essere collegato con qualunque altro nodo nel Graph. I nodi non hanno alcun rapporto libero del genitore-bambino come abbiamo visto nell'albero. Invece i nodi sono denominati come vicini se sono collegati da un bordo. Per esempio, il nodo A qui sopra ha tre vicini: B, C e D.
Non � duro immaginare come la struttura di dati del Graph potrebbe essere utile per rappresentare i dati. Forse ciascuno dei nodi qui sopra potrebbe rappresentare una citt� ed i bordi che collegano i nodi potrebbero rappresentare le strade. O potremmo usare un Graph per rappresentare una rete di calcolatore in cui i nodi sono stazioni di lavoro ed i bordi sono i collegamenti di rete. I Graphs hanno tante applicazioni nell'informatica e nella matematica che parecchie procedure sono state scritte per realizzare i funzionamenti standard del Graph come la ricerca del Graph ed individuazione dello Shortest-Path fra i nodi di un Graph.
Ora che avete un'idea di base della rappresentazione logica dei Graphs, diamo un'occhiata a one-way che i Graphs sono rappresentati comunemente in calcolatori. La rappresentazione � denominata una tabella di adiacenza ed usa l'allineamento bidimensionale per memorizzare le informazioni sui nodi del Graph. La tabella di adiacenza per il nostro Graph � data sotto.
|
|
|
| -- |
1 |
1 |
1 |
-- |
-- |
| 1 |
-- |
1 |
-- |
1 |
-- |
| 1 |
1 |
-- |
-- |
-- |
-- |
| 1 |
-- |
-- |
-- |
1 |
1 |
| -- |
1 |
-- |
1 |
-- |
-- |
| -- |
-- |
-- |
1 |
-- |
-- |
|
|
Notare che la tabella indicata sopra ha sei file e sei colonne identificate con i nodi dal Graph. Contrassegniamo �un 1� in una cellula se esiste un bordo da due nodi che spostano ad incrementi quella cellula. Per esempio, poich� abbiamo un bordo fra A e la B, contrassegniamo �un 1� nelle cellule spostate ad incrementi da A e dal B. Queste cellule sono segnate con una priorit� bassa grigio scuro nella tabella di adiacenza. Con la nostra tabella di adiacenza, possiamo rappresentare ogni bordo possibile che il nostro Graph pu� avere.
|
Keywords:
Graphs programming, graph c++, graph programming, graphing calculator programming, graphs in c++, linear programming graph, graphics programming, graphs tutorial, graphs java
