Synthesis Technology: FM and Wavetable

Synthesis Technology: FM and Wavetable

There are a number of different technologies or algorithms used to create sounds in music synthesizers. Two widely used techniques are Frequency Modulation (FM) synthesis and Wavetable synthesis.

FM synthesis techniques generally use one periodic signal (the modulator) to modulate the frequency of another signal (the carrier). If the modulating signal is in the audible range, then the result will be a significant change in the timbre of the carrier signal. Each FM voice requires a minimum of two signal generators. These generators are commonly referred to as "operators", and different FM synthesis implementations have varying degrees of control over the operator parameters.

Sophisticated FM systems may use 4 or 6 operators per voice, and the operators may have adjustable envelopes which allow adjustment of the attack and decay rates of the signal. Although FM systems were implemented in the analog domain on early synthesizer keyboards, modern FM synthesis implementations are done digitally.

FM synthesis techniques are very useful for creating expressive new synthesized sounds. However, if the goal of the synthesis system is to recreate the sound of some existing instrument, this can generally be done more accurately with digital sample-based techniques.

Digital sampling systems store high quality sound samples digitally, and then replay these sounds on demand. Digital sample-based synthesis systems may employ a variety of special techniques, such as sample looping, pitch shifting, mathematical interpolation, and digital filtering, in order to reduce the amount of memory required to store the sound samples (or to get more types of sounds from a given amount of memory). These sample-based synthesis systems are often called "wavetable" synthesizers (the sample memory in these systems contains a large number of sampled sound segments, and can be thought of as a "table" of sound waveforms which may be looked up and utilized when needed).

Wavetable Synthesis Techniques

The majority of professional synthesizers available today use some form of sampled-sound or Wavetable synthesis. The trend for multimedia sound products is also towards wavetable synthesis. To help prospective MIDI developers, a number of the techniques employed in this type of synthesis are discussed in the following paragraphs.

Looping and Envelope Generation

One of the primary techniques used in wavetable synthesizers to conserve sample memory space is the looping of sampled sound segments. For many instrument sounds, the sound can be modeled as consisting of two major sections: the attack section and the sustain section. The attack section is the initial part of the sound, where the amplitude and the spectral characteristics of the sound may be changing very rapidly. The sustain section of the sound is that part of the sound following the attack, where the characteristics of the sound are changing less dynamically.

Figure 4 shows a waveform with portions which could be considered the attack and the sustain sections indicated. In this example, the spectral characteristics of the waveform remain constant throughout the sustain section, while the amplitude is decreasing at a fairly constant rate. This is an exaggerated example, in most natural instrument sounds, both the spectral characteristics and the amplitude continue to change through the duration of the sound. The sustain section, if one can be identified, is that section for which the characteristics of the sound are relatively constant.

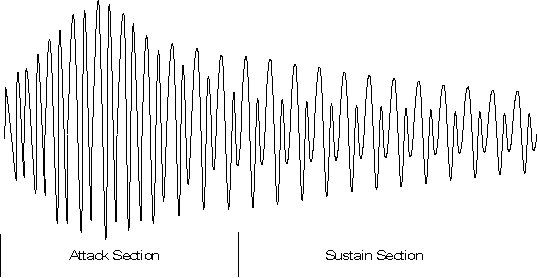
Figure 4: Attack and Sustain Portions of a Waveform

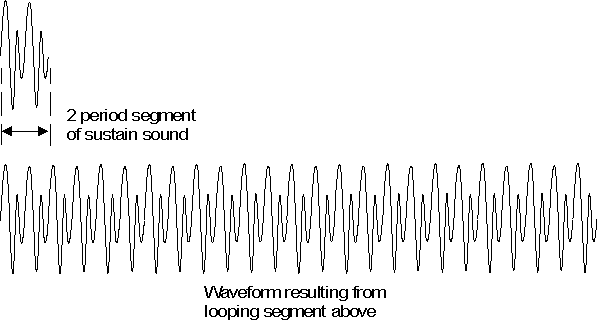
Figure 5: Looping of a Sample Segment

A great deal of memory can be saved in wavetable synthesis systems by storing only a short segment of the sustain section of the waveform, and then looping this segment during playback. Figure 5 shows a two period segment of the sustain section from the waveform in Figure 4, which has been looped to create a steady state signal. If the original sound had a fairly constant spectral content and amplitude during the sustained section, then the sound resulting from this looping operation should be a good approximation of the sustained section of the original.

For many acoustic string instruments, the spectral characteristics of the sound remain fairly constant during the sustain section, while the amplitude of the signal decays. This can be simulated with a looped segment by multiplying the looped samples by a decreasing gain factor during playback to get the desired shape or envelope. The amplitude envelope of a sound is commonly modeled as consisting of some number of linear segments. An example is the commonly used four part piecewise-linear Attack-Decay-Sustain-Release (ADSR) envelope model. Figure 6 depicts a typical ADSR envelope shape, and Figure 7 shows the result of applying this envelope to the looped waveform from Figure 5.

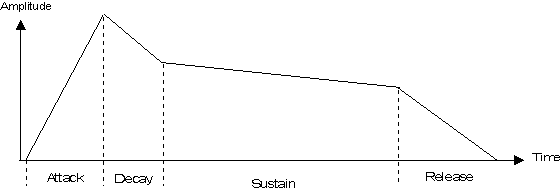
Figure 6: A Typical ADSR Amplitude Envelope

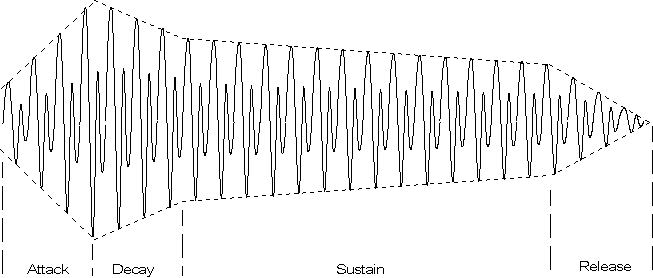
Figure 7: ADSR Envelope Applied to a Looped Sample Segment

A typical wavetable synthesis system would store sample data for the attack section and the looped section of an instrument sound. These sample segments might be referred to as the initial sound and the loop sound. The initial sound is played once through, and then the loop sound is played repetitively until the note ends. An envelope generator function is used to create an envelope which is appropriate for the particular instrument, and this envelope is applied to the output samples during playback.

Playback of the initial wave (with the attack portion of the envelope applied) begins when a Note On message is received. The length of the initial sound segment is fixed by the number of samples in the segment, and the length of the attack and decay sections of the envelope are generally also fixed for a given instrument sound.

The sustain section will continue to repeat the loop samples while applying the sustain envelope slope (which decays slowly in our examples), until a Note Off message is applied. The Note Off message triggers the beginning of the release portion of the envelope.

Loop Length

The loop length is measured as a number of samples, and the length of the loop should be equal to an integral number of periods of the fundamental pitch of the sound being played (if this is not true, then an undesirable "pitch shift" will occur during playback when the looping begins). In practice, the length of the loop segment for an acoustic instrument sample may be many periods with respect to the fundamental pitch of the sound. If the sound has a natural vibrato or chorus effect, then it is generally desirable to have the loop segment length be an integral multiple of the period of the vibrato or chorus.

One-Shot Sounds

The previous paragraphs discussed dividing a sampled sound into an attack section and a sustain section, and then using looping techniques to minimize the storage requirements for the sustain portion. However, some sounds, particularly sounds of short duration or sounds whose characteristics change dynamically throughout their duration, are not suitable for looped playback techniques. Short drum sounds often fit this description. These sounds are stored as a single sample segment which is played once through with no looping. This class of sounds are referred to as "one-shot" sounds.

Sample Editing and Processing

There are a number of sample editing and processing steps involved in preparing sampled sounds for use in a wavetable synthesis system. The requirements for editing the original sample data to identify and extract the initial and loop segments have already been mentioned.

Editing may also be required to make the endpoints of the loop segment compatible. If the amplitude and the slope of the waveform at the beginning of the loop segment do not match those at the end of the loop, then a repetitive "glitch" will be heard during playback of the looped section. Additional processing may be performed to "compress" the dynamic range of the sound to improve the signal/quantizing noise ratio or to conserve sample memory. This topic is addressed next.

When all of the sample processing has been completed, the resulting sampled sound segments for the various instruments are tabulated to form the sample memory for the synthesizer.

Sample Data Compression

The signal-to-quantizing noise ratio for a digitally sampled signal is limited by sample word size (the number of bits per sample), and by the amplitude of the digitized signal. Most acoustic instrument sounds reach their peak amplitude very quickly, and the amplitude then slowly decays from this peak. The ear's sensitivity dynamically adjusts to signal level. Even in systems utilizing a relatively small sample word size, the quantizing noise level is generally not perceptible when the signal is near maximum amplitude. However, as the signal level decays, the ear becomes more sensitive, and the noise level will appear to increase. Of course, using a larger word size will reduce the quantizing noise, but there is a considerable price penalty paid if the number of samples is large.

Compression techniques may be used to improve the signal-to-quantizing noise ratio for some sampled sounds. These techniques reduce the dynamic range of the sound samples stored in the sample memory. The sample data is decompressed during playback to restore the dynamic range of the signal. This allows the use of sample memory with a smaller word size (smaller dynamic range) than is utilized in the rest of the system. There are a number of different compression techniques which may be used to compress the dynamic range of a signal.

Note that there is some compression effect inherent in the looping techniques described earlier. If the loop segment is stored at an amplitude level which makes full use of the dynamic range available in the sample memory, and the processor and D/A converters used for playback have a wider dynamic range than the sample memory, then the application of a decay envelope during playback will have a decompression effect similar to that described in the previous paragraph.

Pitch Shifting

In order to minimize sample memory requirements, wavetable synthesis systems utilize pitch shifting, or pitch transposition techniques, to generate a number of different notes from a single sound sample of a given instrument. For example, if the sample memory contains a sample of a middle C note on the acoustic piano, then this same sample data could be used to generate the C# note or D note above middle C using pitch shifting.

Pitch shifting is accomplished by accessing the stored sample data at different rates during playback. For example, if a pointer is used to address the sample memory for a sound, and the pointer is incremented by one after each access, then the samples for this sound would be accessed sequentially, resulting in some particular pitch. If the pointer increment was two rather than one, then only every second sample would be played, and the resulting pitch would be shifted up by one octave (the frequency would be doubled).

In the previous example, the sample memory address pointer was incremented by an integer number of samples. This allows only a limited set of pitch shifts. In a more general case, the memory pointer would consist of an integer part and a fractional part, and the increment value could be a fractional number of samples. The memory pointer is often referred to as a "phase accumulator" and the increment value is then the "phase increment". The integer part of the phase accumulator is used to address the sample memory, the fractional part is used to maintain frequency accuracy.

For example if the phase increment value was equivalent to 1/2, then the pitch would be shifted down by one octave (the frequency would be halved). A phase increment value of 1.05946 (the twelfth root of two) would create a pitch shift of one musical half-step (i.e. from C to C#) compared with an increment of 1. When non-integer increment values are utilized, the frequency resolution for playback is determined by the number of bits used to represent the fractional part of the address pointer and the address increment parameter.

Interpolation

When the fractional part of the address pointer is non-zero, then the "desired value" falls between available data samples. Figure 8 depicts a simplified addressing scheme wherein the Address Pointer and the increment parameter each have a 4-bit integer part and a 4-bit fractional part. In this case, the increment value is equal to 1 1/2 samples. Very simple systems might simply ignore the fractional part of the address when determining the sample value to be sent to the D/A converter. The data values sent to the D/A converter when using this approach are indicated in the Figure 8, case I.

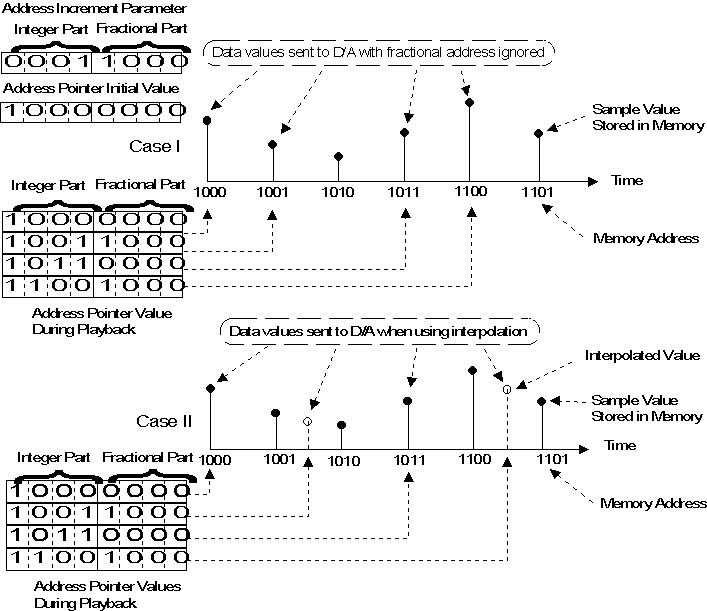
Figure 8: Sample Memory Addressing and Interpolation

A slightly better approach would be to use the nearest available sample value. More sophisticated systems would perform some type of mathematical interpolation between available data points in order to get a value to be used for playback. Values which might be sent to the D/A when interpolation is employed are shown as case II. Note that the overall frequency accuracy would be the same for both cases indicated, but the output is severely distorted in the case where interpolation is not used.

There are a number of different algorithms used for interpolation between sample values. The simplest is linear interpolation. With linear interpolation, interpolated value is simply the weighted average of the two nearest samples, with the fractional address used as a weighting constant. For example, if the address pointer indicated an address of (n+K), where n is the integer part of the address and K is the fractional part, than the interpolated value can be calculated as s(n+K) = (1-K)s(n) + (K)s(n+1), where s(n) is the sample data value at address n. More sophisticated interpolation techniques can be utilized to further reduce distortion, but these techniques are computationally expensive.

Oversampling

Oversampling of the sound samples may also be used to improve distortion in wavetable synthesis systems. For example, if 4X oversampling were utilized for a particular instrument sound sample, then an address increment value of 4 would be used for playback with no pitch shift. The data points chosen during playback will be closer to the "desired values", on the average, than they would be if no oversampling were utilized because of the increased number of data points used to represent the waveform. Of course, oversampling has a high cost in terms of sample memory requirements.

In many cases, the best approach may be to utilize linear interpolation combined with varying degrees of oversampling where needed. The linear interpolation technique provides reasonable accuracy for many sounds, without the high penalty in terms of processing power required for more sophisticated interpolation methods. For those sounds which need better accuracy, oversampling is employed. With this approach, the additional memory required for oversampling is only utilized where it is most needed. The combined effect of linear interpolation and selective oversampling can produce excellent results.

Splits

When the pitch of a sampled sound is changed during playback, the timbre of the sound is changed somewhat also. The effect is less noticeable for small changes in pitch (up to a few semitones), than it is for a large pitch shift. To retain a natural sound, a particular sample of an instrument sound will only be useful for recreating a limited range of notes. To get coverage of the entire instrument range, a number of different samples, each with a limited range of notes, are used. The resulting instrument implementation is often referred to as a "multisampled" instrument. This technique can be thought of as splitting a musical instrument keyboard into a number of ranges of notes, with a different sound sample used for each range. Each of these ranges is referred to as a split, or key split.

Velocity splits refer to the use of different samples for different note velocities. Using velocity splits, one sample might be utilized if a particular note is played softly, where a different sample would be utilized for the same note of the same instrument when played with a higher velocity. This technique is not commonly used to produce basic sound samples because of the added memory expense, but both key splitting and velocity splitting techniques can be utilized as a performance enhancement. For instance, a key split might allow a fretless bass sound on the lower octaves of a keyboard, while the upper octaves play a vibraphone. Similarly, a velocity split might "layer" strings on top of an acoustic piano sound when the keys are hit with higher velocity.

Aliasing Noise

Earlier paragraphs discussed the timbre changes which result from pitch shifting. The resampling techniques used to shift the pitch of a stored sound sample can also result in the introduction of aliasing noise into an instrument sound. The generation of aliasing noise can also limit the amount of pitch shifting which may be effectively applied to a sound sample. Sounds which are rich in upper harmonic content will generally have more of a problem with aliasing noise. Low-pass filtering applied after interpolation can help eliminate the undesirable effect of aliasing noise. The use of oversampling also helps eliminate aliasing noise.

LFOs for Vibrato and Tremolo

Vibrato and tremolo are effects which are often produced by musicians playing acoustic instruments. Vibrato is basically a low-frequency modulation of the pitch of a note, while tremolo is modulation of the amplitude of the sound. These effects are simulated in synthesizers by implementing low-frequency oscillators (LFOs) which are used to modulate the pitch or amplitude of the synthesized sound being produced.

Natural vibrato and tremolo effects tend to increase in strength as a note is sustained. This is accomplished in synthesizers by applying an envelope generator to the LFO. For example, a flute sound might have a tremolo effect which begins at some point after the note has sounded, and the tremolo effect gradually increases to some maximum level, where it remains until the note stops sounding.

Layering

Layering refers to a technique in which multiple sounds are utilized for each note played. This technique can be used to generate very rich sounds, and may also be useful for increasing the number of instrument patches which can be created from a limited sample set. Note that layered sounds generally utilize more than one voice of polyphony for each note played, and thus the number of voices available is effectively reduced when these sounds are being used.

Digital Filtering

It was mentioned earlier that low-pass filtering may be used to help eliminate noise which may be generated during the pitch shifting process. There are also a number of ways in which digital filtering is used in the timbre generation process to improve the resulting instrument sound. In these applications, the digital filter implementation is polyphonic, meaning that a separate filter is implemented for each voice being generated, and the filter implementation should have dynamically adjustable cutoff frequency and/or Q.

For many acoustic instruments, the character of the tone which is produced changes dramatically as a function of the amplitude level at which the instrument is played. For example, the tone of an acoustic piano may be very bright when the instrument is played forcefully, but much more mellow when it is played softly. Velocity splits, which utilize different sample segments for different note velocities, can be implemented to simulate this phenomena.

Another very powerful technique is to implement a digital low-pass filter for each note with a cutoff frequency which varies as a function of the note velocity. This polyphonic digital filter dynamically adjusts the output frequency spectrum of the synthesized sound as a function of note velocity, allowing a very effective recreation of the acoustic instrument timbre.

Another important application of digital filtering is in smoothing out the transitions between samples in key-based splits. At the border between two splits, there will be two adjacent notes which are based on different samples. Normally, one of these samples will have been pitch shifted up to create the required note, while the other will have been shifted down in pitch. As a result, the timbre of these two adjacent notes may be significantly different, making the split obvious. This problem may be alleviated by employing a digital filter which uses the note number to control the filter characteristics. A table may be constructed containing the filter characteristics for each note number of a given instrument. The filter characteristics are chosen to compensate for the pitch shifting associated with the key splits used for that instrument.

It is also common to control the characteristics of the digital filter using an envelope generator or an LFO. The result is an instrument timbre which has a spectrum which changes as a function of time. An envelope generator might be used to control the filter cutoff frequency generate a timbre which is very bright at the onset, but which gradually becomes more mellow as the note decays. Sweeping the cutoff frequency of a filter with a high Q setting using an envelope generator or LFO can help when trying to simulate the sounds of analog synthesizers.