|
La derni�re structure de donn�es que nous �tudierons dans ce cours d'instruction est les graphiques. Les graphiques sont semblables aux arbres sauf que, ils n'ont pas autant de restrictions. Dans le cours d'instruction pr�c�dent, nous avons vu que chaque arbre a un noeud de racine, et tous autres noeuds dans l'arbre sont des enfants d'un noeud perticular. Nous avons �galement vu que les noeuds peuvent avoir beaucoup d'enfants mais seulement un parent. Quand nous d�tendons ces restrictions, nous obtenons la structure de donn�es de graphique. La repr�sentation logique d'un graphique typique pourrait sembler quelque chose comme la figure montr�e ci-dessous :
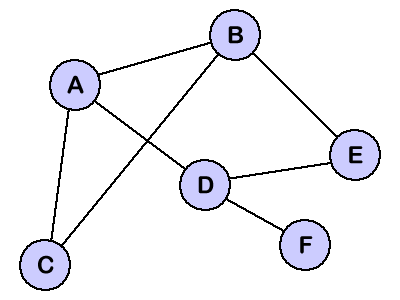
Noter que notre graphique n'a aucun noeud de racine comme la structure de donn�es d'arbre. Au lieu de cela, n'importe quel noeud peut �tre reli� � n'importe quel autre noeud dans le graphique. Les noeuds n'ont aucun rapport clair de parent-enfant comme nous voyions dans l'arbre. Au lieu de cela des noeuds s'appellent comme voisins s'ils sont reli�s par un bord. Par exemple, le noeud A ci-dessus a trois voisins : B, C, et D.
Il n'est pas difficile d'imaginer comment la structure de donn�es de graphique pourrait �tre utile pour repr�senter les donn�es. Peut-�tre chacun des noeuds ci-dessus pourrait repr�senter une ville et les bords reliant les noeuds pourraient repr�senter les routes. Ou nous pourrions employer un graphique pour repr�senter un r�seau informatique o� les noeuds sont des postes de travail et les bords sont les raccordements de r�seau. Les graphiques ont tant d'applications dans l'informatique et les math�matiques que plusieurs algorithmes ont �t� �crits pour effectuer les op�rations standard de graphique telles que rechercher le graphique et trouver le Shortest-Path entre les noeuds d'un graphique.
Maintenant que vous avez une id�e fondamentale de la repr�sentation logique des graphiques, jetons un coup d'oeil � l'one-way que des graphiques sont g�n�ralement repr�sent�s dans des ordinateurs. La repr�sentation s'appelle une matrice de contigu�t�, et elle emploie la rang�e bidimensionnelle pour stocker les informations sur les noeuds de graphique. La matrice de contigu�t� pour notre graphique est donn�e ci-dessous.
|
|
|
| -- |
1 |
1 |
1 |
-- |
-- |
| 1 |
-- |
1 |
-- |
1 |
-- |
| 1 |
1 |
-- |
-- |
-- |
-- |
| 1 |
-- |
-- |
-- |
1 |
1 |
| -- |
1 |
-- |
1 |
-- |
-- |
| -- |
-- |
-- |
1 |
-- |
-- |
|
|
Noter que la matrice montr�e ci-dessus a six rang�es et six colonnes marqu�es avec les noeuds du graphique. Nous marquons un � 1 � dans une cellule si l� existe un bord de deux noeuds qui classent cette cellule. Par exemple, puisque nous avons un bord entre A et B, nous marquons un � 1 � dans les cellules class�es par A et le B. Ces cellules sont identifi�es par un fond gris-fonc� dans la matrice de contigu�t�. Avec notre matrice de contigu�t�, nous pouvons repr�senter chaque bord possible que notre graphique peut avoir.
|
Keywords:
Graphs programming, graph c++, graph programming, graphing calculator programming, graphs in c++, linear programming graph, graphics programming, graphs tutorial, graphs java
