Polynomials
A D V E R T I S E M E N T
In Matlab, a polynomial is represented by a vector. To create a polynomial in
Matlab, simply enter each coefficient of the polynomial into the vector in
descending order. For instance, let's say you have the following polynomial:
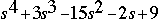
To enter this into Matlab, just enter it as a vector in the following manner
x = [1 3 -15 -2 9] x = 1 3 -15 -2 9
Matlab can interpret a vector of length n+1 as an nth order polynomial. Thus, if
your polynomial is missing any coefficients, you must enter zeros in the
appropriate place in the vector. For example,
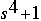
would be represented in Matlab as:
You can find the value of a polynomial using the polyval function. For
example, to find the value of the above polynomial at s=2,
z = polyval([1 0 0 0 1],2) z = 17
You can also extract the roots of a polynomial. This is useful when you have
a high-order polynomial such as
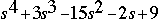
Finding the roots would be as easy as entering the following command;
roots([1 3 -15 -2 9]) ans = -5.5745 2.5836 -0.7951 0.7860
Let's say you want to multiply two polynomials together. The product of two
polynomials is found by taking the convolution of their coefficients. Matlab's
function conv that will do this for you.
x = [1 2]; y = [1 4 8]; z = conv(x,y) z = 1 6 16 16
Dividing two polynomials is just as easy. The deconv function will
return the remainder as well as the result. Let's divide z by y and see if we
get x.
[xx, R] = deconv(z,y) xx = 1 2 R = 0 0 0 0
As you can see, this is just the polynomial/vector x from before. If y had not
gone into z evenly, the remainder vector would have been something other than
zero.If you want to add two polynomials together which have the same order, a
simple z=x+y will work (the vectors x and y must have the same length). In the
general case, the user-defined function, polyadd
can be used. To use polyadd, copy the function into an
m-file, and
then use it just as you would any other function in the Matlab toolbox. Assuming
you had the polyadd function stored as a m-file, and you wanted to add the two
uneven polynomials, x and y, you could accomplish this by entering the command:
z = polyadd(x,y) x = 1 2 y = 1 4 8
z = 1 5 10
|
