Liabilities
A D V E R T I S E M E N T
Liabilities are essentially debts. They can be:
current (short term): due & payable within 1 year
long-term: due & payable in over 1 year
The most common liabilities are:
Accounts Payable: for routine expenses and inventory purchased
on credit
Notes Payable: short- or long-term loans from banks or other
lenders
Accrued Expenses: various current expenses, accrued to
prepare financial statements; these can include accounts such as interest
payable, taxes payable, wages payable, and other similar accruals at the end of
the year.
Mortgage Notes: long term borrowing to purchase major assets;
the assets purchased are also pledged as collateral
Bonds Payable: corporation general debt; bonds of major
corporations can be purchased on a public stock exchange; bonds pay interest on
a regular basis, usually twice a year; bonds may have maturity dates from 5 to
30 years, or any other time frame selected by the company and acceptable by
lenders.
Liabilities often have to be estimated at balance sheet date,
so we can prepare financial statements.
Amortization table
An amortization table is a calculation involving interest and
regular payments, or reductions, in an account or debt. Costs can be amortized
over several years, using an amortization table. They are usually prepared to
show the progress of loan payments, especially in long-term mortgage loans. If
you have a home loan, you will probably get an amortization table from your
bank, showing how your payments are divided among interest, principle and other
fees (escrow).
Amortization tables are relatively easy to prepare. The use
of computer spreadsheet programs makes creating these tables a very simple task.
One "template" can be created and used over and over for different amounts,
interest rates and time frames.
Interest calculation
Interest applies to many liabilities. Notes, bonds and mortgages
all involve interest.
Interest is the fee you pay for the use of someone else's
money. The calculation is always the same.
| IInterest
= Principle X
Annual Interest Rate
X Time (portion of
a year) |
Interest Rates are always expressed in annual terms. For
instance, 12% interest means 12% per year, or 1% (1/12) per month.
The Time factor is always in relation to a year, so it
maintains the correct relationship with annual interest rates. One month's time
factor would be 1/12. Three months' would be 3/12, 7 months would be 7/12, etc.
Sometimes interest agreements are expressed in a number of
days. We usually use a 360 day year to make the calculation easier, and more
rounded. This goes back to the days before modern calculators and computers,
when we used pencil and paper to calculate interest. Example: 30 day note uses
30/360 time factor.
Using Amortization Tables
Amortization is an accounting method used to spread costs or
payments over a period of time, based on a few basic concepts: Time, Principal
(money or cost), and Interest Rate. Amortizing a loan balance uses all three of
these to reduce a loan balance to zero over a number of years. This might apply
to a home mortgage or automobile loan. It might also apply to an automobile or
equipment lease.
Interest is always expressed as an annual Rate, so your
interest calculation must always have a Time factor. For instance, one year's
interest on $100 at 12% (annual rate) is
$100 x 12% = $12 annual interest [on your calculator 100 *
.12 = 12]
If you make a home or car loan payment every month, you would
not want to pay a year's worth of interest on each monthy payment, would you?
(this is not a trick question ;-) Of course, you would only want to pay one
month's interest each month. So we have to add a Time factor to the annual
interest calculation above. In this case there are 12 months in a year, to
calculate one month's interest we would use 1/12 as a Time factor.
$100 x 12% x 1/12 = $1 monthly interest [100 * .12 / 12 * 1=
1]
If you wanted to calculate interest for 2 months you would
use 2/12:
$100 x 12% x 2/12 = $2 interest [100 * .12 / 12 * 2 = 2]
The monthly payment amount stays the same each month, and is
divided between interest expense and principal reduction. As the principal goes
down, so does the interest expense. Eventually the principal amount is zero,
perhaps over 5 years for a car loan, or 25 years for a home mortgage.
Let's say you buy a new home with a $100,000 mortgage, spread
over 25 years, at 8% interest. How much is your payment going to be, and how
much interest will you pay over the life of the loan if you make all the
payments on time? Here's a good website you can visit to answer this type of
question.
http://www.interest.com/calculators
I used their calculator to answer this question, and create
an amortization table. It took about 10 seconds. Your monthly payment would be
$771.82 and your total interest over the life of the loan (25 years) would be
$131,542.40. In total your $100,000 loan would cost you $231, 542.40 -- that's
over twice the amount of money you originally borrowed, in fact you would pay
back 2.3 times your original loan amount.
Many borrowers reduce their overall interest expense by
making extra principal payments on their loans whenever possible. Look at an
amortization table you will see that most of the monthly payment goes to
Interest and only a small portion goes to Principal Reduction. [If you have not
done so yet, use the calculator link, and enter the amounts shown above, then
generate an amortization table and look at it.]
At the end of month 1, you would have paid $771.82 ($666.67
interest and $105.15 principal). This reduces your principal balance to
$99,894.85. If you were to make all the first 12 payments on time you would have
paid $9,261.84 ($7952.69 interest and $1309.15 principal.) At the end of 12
months the loan balance would be $98,690.85. Now, follow closely at this point.
| Principal balance after month 1 |
$99,894.85
|
| Principal balance after month 12 |
$98,690.85
|
| Difference |
$1,204.00
|
| Month 1 payment |
$771.82
|
| Total payment |
$1975.82
|
If I pay and extra $1204 principal in month 1, it will reduce
my principal balance and move me down the amortization table to where I would be
after 12 months. I would avoid paying the amortized interest for months 2 - 12,
a savings of $7286.02 over the life of the loan.
In other words, paying an extra $1204 principal saved me
$7286 in interest. It would also reduce my total loan payments by 1 year,
because I moved down 12 months on the amortization table.
An alternative: Let's say you can't afford to pay that much
extra principal each month. If you move down the amortization table one extra
month, and pay just that amount of extra principal, you would cut your total
interest (about) in half, and cut the loan payoff time in half. In this example
you would reduce the loan from 25 years to 12.5 years, and reduce your total
interest from $131,542.40 to (about) $65,771.20 - a huge savings!!
CAVEAT: You must still make monthly loan payments, even if
you pay off some principal early. So you should incorporate extra principal
reduction strategies into your overall cashflow budget. But the earlier you
reduce your principal, the better.
Using a spreadsheet, you can quickly create an amortization
table for any principal amount, interest rate, payment amount or time factor.
With a spreadsheet you can quickly see how different interest rates and payment
schedules can effect your personal finances. You can use it for credit cards as
well. The same concepts apply.
Preparing and using an Amortization Table, year-end balances and adjusting
journal entries
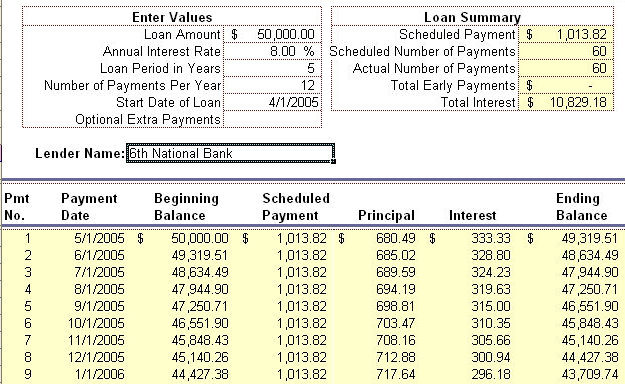
On April 1, 2005, Mike's Bikes, Inc. signed a 5-year, $50,000 note payable to
6th National Bank in conjunction with the purchase of equipment. The note calls
for interest at an annual rate of 8%, with payments of $ 1,013.82 per month
starting May 1, 2005. The note is fully amortizing over a period of 60 months.
The bank sent Mike an amortization table showing the allocation of monthly
payments between interest and principal over the life of the loan. A small part
of this amortization table is illustrated below.
In Chapter 7 we prepared a Bank Reconciliation to dertermine the correct Cash
account balance. We also entered journal entries to correct any errors and
journalize any unrecorded transactions.
In Chapter 10 we are going to verify the correct account balances for Notes
Payable and Interest Payable, that is, the balance these accounts should be
as of year-end on December 31. This is one of our standard and ordinary year-end
procedures.
We determine correct loan and interest payable balances by creating an
amortization table. We will write adjusting entries to bring the account
balances into agreement with the amortization table.
Let's look at some journal entries over the life of a loan and see how
they relate to the amortization table.
Journal entry to record the original note payable of $50,000 on April
1, 2005. We have increased Cash (Debit) and increased Notes Payable (Credit). No
interest has accrued yet. Interest is related to time, so at least one day must
pass before we can calculate (accrue) interest.
| Date |
Account |
Debit |
Credit |
| Apr-1 |
Cash |
$50,000 |
|
| |
Notes Payable |
|
$50,000 |
| |
To record 8% 60-month note with
6th National Bank |
|
|
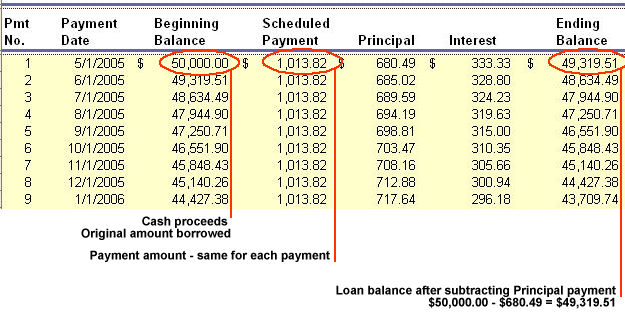
Monthly payments and principal balances
Interest calculation
Beginning Balance * Annual Interest Rate * Time Factor
$50,000 * 8% * 1/12 = $333.33
Principal payment = Payment amount - Interest
$1,013.82 - $333.33 = $680.49
Principal balance reduction
Beginning Balance - Principal payment = Ending Balance
$50,000 - $680.49 = $49,319.51
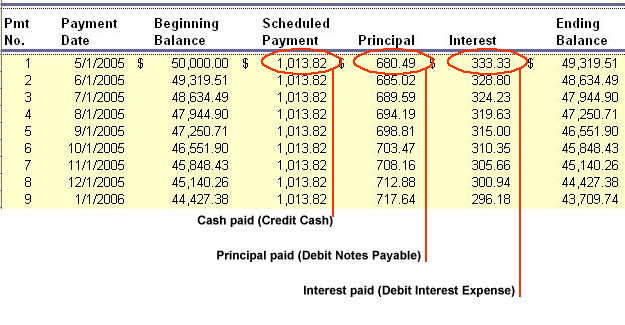
Journal entry to record the first monthly payment on this note, May 1,
2005, payment 1 from the amortization table above.
| Date |
Account |
Debit |
Credit |
| May-1 |
Notes Payable |
$680.49 |
|
| |
Interest Expense |
333.33 |
|
| |
Cash |
|
$1013.82 |
| |
To record monthly note payment for May. |
|
|
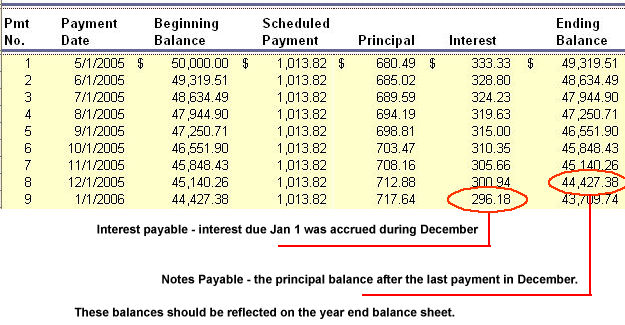
Balances at December 31, 2006 (year end)
Making Year-End Adjusting Journal Entries
Adjusting journal entries should be made to bring account balances to the
correct amount before preparing financial statements. The Books are not always
correct or accurate. This situation needs to be corrected at the end of the
year, or anytime we need to prepare Financial Statements
At the end of each year we organize our adjusting entries on a Working Trial
Balance (WTB) before preparing financial statements. You can see an example of
the WTB in Comprehensive Problem 1, in your text. Let's look at an example of
year-end adjusting entries.
Example - adjusting Notes Payable at year-end
Assume the following: We look at the WTB and see that the loan balance is
recorded as a credit balance of $ 44,329.16. We compare this with our
amortization table and see that the correct balance should be a credit balance
of $ 44,427.38. We need to make an adjusting entry to bring the books to the
correct balance.
In this case we need to credit Notes Payable for $ 98.22 to bring the
books into agreement with the amortization table. In some cases we would have to
debit Notes Payable. When do you think that would be the case? If an
amortization table was used for each monthly loan payment, the books should
agree with the amortization table, and no adjusting entry would be needed in
that case.
What account should we debit? We must review the related journal entries for
the year and see which accounts were debited and credited each month. In most
cases we will make the adjustment to the Interest Expense account (look at the
monthly entries above). In some cases we may find that a different account was
used by mistake. We would correct that error as well, when making the year end
adjustments. Let's assume that the only two accounts effected in this example
are Notes Payable and Interest Expense. The adjusting journal entry would be.
| Date |
Account |
Debit |
Credit |
| Dec-31 |
Interest Expense |
$ 98.22 |
|
| |
Notes Payable |
|
$ 98.22 |
| |
To adjust Notes Payable to agree with amortization table |
|
|
Proof:
| |
Debit
|
Credit
|
| Notes Payable balance |
|
44,329.16
|
| Adjustment |
|
98.22
|
| Corrected NP balance |
|
44,427.38
|
| Balance per amortization table |
|
44,427.38
|
| Difference |
|
0
|
The same approach can be used to reconcile and adjust Interest Expense. But
generally speaking we are more concerned with having the correct Notes Payable
balance on the balance sheet.
Large businesses record transactions daily, sometimes in Real Time, as they
happen. Smaller businesses may record transactions less frequently, perhaps at
the end of the day, week or month. Bookkeepers often have to make estimates,
especially when they don't have enough information to write a correct entry.
This is common in the business world.
Here's a common example, and one I see on a regular basis as an accountant
and tax preparer. A client or their bookkeeper records a loan payment as a debit
to "Loan Payment" and a credit to "Cash." You should know by now that
accountants don't use an account called "Loan Payment." We record a loan payment
with debits to Interest Expense and Notes Payable and a credit to Cash, as shown
in the examples above. To correct the bookkeeper's error we would write an
adjusting entry to debit the correct accounts and bring the "bogus" account to a
zero balance.
Present Value
If you owe me $1000 I would like to have it paid as soon as
possible. I am losing the use of my money as long as you owe me.
If I fall on hard times I might prefer to get my money paid
back sooner, rather than later, because I need the money now. I might be
inclined to settle for less than the full amount of the debt, in order to get
the cash I need as soon as possible.
Let's say I could earn 10% interest if I had the money you
owe me. In one year I would lose:
$1000 x 10% x 1 = $100 interest
if you paid me back now I could accept
$1000 - $100 = $900
Investing that money in an interest bearing account, which
compounds daily (typical bank method), the $900 would grow to $1000 in a year. I
would be in the same position at the end of a year, either way. But one way I
have my money available in case I need it, which may be preferable.
The long and short of this story is simple. Money has a
value, over time. It can be calculated fairly easily. If we don't have our
money, we lose the use of it. Having money now is better than having it in the
future, because I can put it to better use if it is available to me.
The business world accepts these simple facts about money,
and business managers assume that interest should be earned or paid whenever
appropriate in the situation. Federal tax law mandates that interest be charged
where appropriate. Zero interest loans are not recognized for federal tax
purposes.
Contingencies
A contingent situation is one that may arise in the future,
based on some past event. For instance, if I sell lawnmowers one of them might
break in the warranty period, and I will have to replace it. The warranty claim
will arise in the future, from a sale made today.
There may be contingent gains or losses. Contingent gains are
ignored until they are finalized. Contingent losses are recognized as soon as
they can be identified and measured.
GAAP places a couple of requirements on contingent losses.
They should be reported in the financial statements if they meet BOTH of two
criteria:
1) the loss is probable,
2) the amount can be reasonably estimated.
It must also be a material amount, in order to have a
reportable effect on the financial statements. Some are just a normal part of
business, called general business risk, and are not reported. For instance, we
all know that airplanes can crash. Airlines don't consider this a reportable
contingency, because it is impossible to predict the occurrence or amount of
loss in advance.
On the other hand, the company may be involved in a lawsuit.
Their attorney advises them that they will probably lose, based on other cases
and the probable loss will be $100,000. The loss is probable, and the amount can
be reasonably estimated. The loss would be entered into the books, with a
journal entry, and disclosed in the financial statements.
|
