|
Die letzte Datenstruktur, die wir in diesem Tutorial studieren, ist die Diagramme. Diagramme sind B�umen �hnlich, au�er da�, sie haben nicht da viele Beschr�nkungen. Im vorhergehenden Tutorial sahen wir, da� jeder Baum einen Wurzelnullpunkt hat, und alle anderen Nullpunkte im Baum sind Kinder eines perticular Nullpunktes. Wir sahen auch, da� die Nullpunkte viele Kinder aber nur ein Elternteil haben k�nnen. Wenn wir diese Beschr�nkungen uns entspannen, erhalten wir die DiagrammDatenstruktur. Die logische Darstellung eines typischen Diagramms konnte etwas wie die Abbildung schauen, die unten gezeigt wurde:
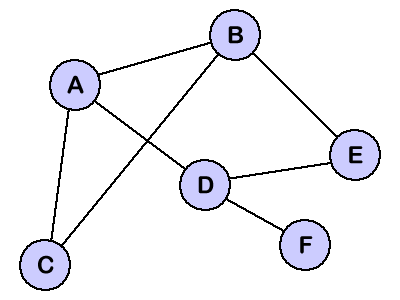
Beachten, da� unser Diagramm keinen Wurzelnullpunkt wie die BaumDatenstruktur hat. Stattdessen kann jeder m�glicher Nullpunkt mit irgendeinem anderen Nullpunkt im Diagramm angeschlossen werden. Nullpunkte haben kein freies Elternteilkind Verh�ltnis, wie wir in den Baum sahen. Stattdessen werden Nullpunkte als Nachbarn benannt, wenn sie durch einen Rand angeschlossen werden. Z.B. hat Nullpunkt A oben drei Nachbarn: B, C und D.
Es ist nicht hart, sich vorzustellen, wie die DiagrammDatenstruktur f�r das Darstellen der Daten n�tzlich sein k�nnte. M�glicherweise k�nnte jeder der Nullpunkte oben eine Stadt darstellen und die R�nder, welche die Nullpunkte anschlie�en, konnten die Stra�en darstellen. Oder wir k�nnten ein Diagramm benutzen, um ein Computernetz darzustellen, in dem die Nullpunkte Workstationen sind und die R�nder die Network Connections sind. Diagramme haben so viele Anwendungen in der Informatik und der Mathematik, da� einige Algorithmen geschrieben worden sind, um die Standarddiagrammbetriebe wie Suchen des Diagramms und Finden des Shortest-Path zwischen Nullpunkten eines Diagramms durchzuf�hren.
Nun da du eine Grundidee der logischen Darstellung der Diagramme hast, lassen Sie uns einen Blick am One-way nehmen, da� Diagramme allgemein in den Computern dargestellt werden. Die Darstellung wird eine Angrenzenmatrix genannt, und sie verwendet die zweidimensionale Reihe, um die Informationen �ber die Diagrammnullpunkte zu speichern. Die Angrenzenmatrix f�r unser Diagramm wird unten gegeben.
|
|
|
| -- |
1 |
1 |
1 |
-- |
-- |
| 1 |
-- |
1 |
-- |
1 |
-- |
| 1 |
1 |
-- |
-- |
-- |
-- |
| 1 |
-- |
-- |
-- |
1 |
1 |
| -- |
1 |
-- |
1 |
-- |
-- |
| -- |
-- |
-- |
1 |
-- |
-- |
|
|
Beachten, da� die Matrix, die oben gezeigt wird, sechs Reihen und sechs Spalten hat, die mit den Nullpunkten vom Diagramm beschriftet werden. Wir kennzeichnen �1� in einer Zelle, wenn ein Rand von zwei Nullpunkten besteht, die diese Zelle registrieren. Z.B. da wir einen Rand zwischen A und B haben, kennzeichnen wir �1� in den Zellen, die durch A und B. registriert werden. Diese Zellen werden mit einem dunkelgrauen Hintergrund in der Angrenzenmatrix gekennzeichnet. Mit unserer Angrenzenmatrix k�nnen wir jeden m�glichen Rand darstellen, den unser Diagramm haben kann.
|
Schl�sselw�rter: Die Diagramme, die, Diagramm c++, die Diagrammprogrammierung, den Rechner programmiert, Diagramme in c++, lineares programmierendiagramm, die programmierenden Graphiken graphisch darstellend programmieren, stellt Tutorial, Diagramme Java graphisch dar
